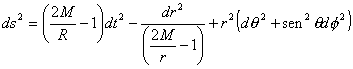|
||||||||||||||||||||||||
|
3-
PROPRIEDADES DOS BURACOS NEGROS Esse buraco negro surge da solução das equações de Einstein para o vácuo com simetria esférica, as quais foram derivadas pela primeira vez por Karl Schwarzschild em 1916, a apenas alguns meses depois da publicação das equações de Einstein. Esse buraco negro é caracterizado completamente pelo parâmetro M, o qual é identificado como a sua massa quando vista por um observador distante. Vejamos agora algumas de suas propriedades. 3.1- GEODÉSICAS Na física Newtoniana, a gravitação é representada por uma interação a distância entre as partículas massivas. Já em relatividade geral, a interação não é representada por uma interação diretamente entre as partículas massivas. Na verdade cada partícula massiva deforma a geometria do espaço-tempo ao seu redor desviando assim a trajetória das demais partículas que se aproximem dela, e vice-versa. Logo, esse desvio da trajetória das partículas devido a curvatura do espaço-tempo e que representa nessa teoria a interação gravitacional. Assim, diferentemente do espaço-tempo da relatividade Especial, o espaço-tempo da relatividade geral é curvo. Na relatividade especial, nós sabemos que trajetória de partículas livres são retas, já na relatividade geral isso não é possível pois o espaço-tempo é curvo, e não plano. A relatividade geral nos fornece as equações necessárias para identificarmos as trajetórias seguidas por partículas livres no espaço-tempo as quais são chamadas de geodésicas. As geodésicas podem ser de dois tipos: nulas para o caso da trajetória de partículas sem massa (ds²=0), e tipo-tempo para o caso da trajetória de partículas massivas (ds²=1). Vamos nos deter em detalhes na determinação das geodésicas tipo-tempo as do tipo nula poderão ser obtidas de forma análoga.
As equações da geodésica são 4 e temos além disso a condição ds²=1.
Temos 4 variáveis a determinar: t=t(t),
r=r(t), θ=θ(t)
e f=f(t),
onde (t,r,θ,f)
são as coordenadas esféricas mais o tempo em termos dos quais
escrevemos o espaço-tempo de Schwarzschild, e
t é
o tempo próprio o qual é parâmetro afim apropriado para descrever
trajetórias tipo-tempo. Poderemos então escolher as 5 equações as 4
mais simples. Consideremos que o movimento se dá sobre um plano, por
simplicidade escolhamos o plano equatorial: θ
= π/2. Se introduzirmos essa escolha nas nossas equações,
obtemos que uma vez introduzido as constantes de integração L e
E, respectivamente momento angular e energia. Essas duas dão o
valor de f
e t em
função de r. Substituindo esses valores na última equação
obtemos uma equação para r aonde só comparecem termos em r.
Ela pode ser escrita na forma de uma primeira integral do
movimento
onde
o potencial V²(r) é dado por,
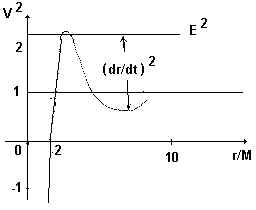
A equação (4) difere da equação padrão em física Newtoniana para a primeira integral do movimento pelos termos em V² e E² ao invés de V e E. Podemos construir o gráfico de V ²x r para um valor de L fixo, o que dá
Fig.
1
Vamos listar algumas das propriedades mais importantes
dessas geodésicas.
|
A grande diferença entre a presente situação e o caso análogona gravitação Newtoniana (partícula sobre ação de uma massa M localizada em r = 0) é a presença do poço infinito em V² acima para valores de r próximos de r=0. No caso Newtoniano tínhamos uma barreira infinita que impedia a aproximação das partículas de r=0. 3.2 -
SINGULARIDADE E HORIZONTE DE EVENTOS
Notamos que gab não está bem definida em dois valores de r (suas componentes divergem - algumas delas) : r = 2M e r = 0. A superfície r = 2M (bidimensional) é o chamado horizonte de eventos, e não é de fato uma singularidade pois em outros sistemas de coordenadas a métrica se comporta bem sobre essa superfície. A primeira propriedade interessante dessa superfície que gostaríamos de mencionar é que usando a relatividade geral podemos recuperar o resultado de Laplace eq.(3) e verificar que o nome de buraco negro se encaixa bem a solução de Schwarzschild. Para isso suponha que enviamos radiação eletromagnética do horizonte de eventos para um observador distante r >> 2M. Se a freqüência da radiação medida por um observador no horizonte é r H e a freqüência medida pelo observador distante é rd, podemos relacionar as duas em relatividade geral, no caso de espaço-tempo estáticos por,
Substituindo os valores
de g00 da equação (6), obtemos que,
ou seja, todas as freqüências são fortemente desviadas para o vermelho. Assim, o observador não irá ver em um tempo finito essa radiação emitida do horizonte. Essa superfície marca a região a partir de onde nada nem a luz pode escapar o que acontece para r < 2M. Em relatividade especial identificamos a coordenada temporal observando quais das componentes da métrica é negativa. O mesmo é válido para Schhwarzschild eq.(6). Só que ao cruzarmos o horizonte em direção a r = 0, notamos que o elemento de linha eq.(6) fica reescrito como,
E para r <2M, a coordenada radial é que faz o papel de tempo enquanto que t é uma coordenada espacial! r = 0 é realmente uma singularidade física, não pode ser removida através de uma transformação de coordenadas. Esse fato traz problemas para a relatividade geral pois em r =0 a curvatura do espaço-tempo diverge e as equações de Einstein perdem o seu poder de previsibilidade. Uma solução para esse problema é que supor que a região em que r <2M, dentro do horizonte, está isolada do resto do espaço-tempo (o que é de fato razoável pois não temos informações sobre o que acontece lá dentro), e fora do domínio de previsibilidade da relatividade geral. E se tivéssemos uma outra singularidade do tipo de r =0, aparecendo em outra solução das equações de Einstein, só que sem o horizonte a envolvendo? ou seja as chamadas singularidades nuas? Para evitar esse tipo de situação Roger Penrose propôs o chamado "Cosmic Censorship Confecture" que propõem que sempre que uma singularidade física se forma, juntamente se forma um horizonte de eventos a envolvendo. Ao estudarmos as geodésicas do tipo-tempo notamos que quando uma partícula atravessa o horizonte na direção de r =0, ela não pode mais retornar. Podemos ter uma visão mais clara desse efeito analisando o elemento de linha eq.(9). Como r descreve a passagem do tempo dentro do horizonte, temos que o decréscimo em r representa o avanço nos relógios. Assim, se tentássemos retornar para r = 2M estaríamos voltando no tempo o que não é possível. Logo todas as partículas que entravam no horizonte necessariamente vão se encontrar com a singularidade r = 0 em seus futuros.
|
|||||||||||||||||||||||
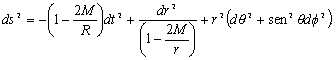
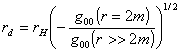 .
.